$ R_Y(\alpha) = \left[ \begin{array}{ccc} \cos(\alpha) & 0 & \sin(\alpha) \\ 0 & 1 & 0 \\ -\sin(\alpha) & 0 & \cos(\alpha) \end{array} \right]$¶
$ R_X(\beta) = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos(\beta) & -\sin(\beta) \\ 0 & \sin(\beta) & \cos(\beta) \end{array} \right]$¶
$ R_Z(\gamma) = \left[ \begin{array}{ccc} \cos(\gamma) & -\sin(\gamma) & 0 \\ \sin(\gamma) & \cos(\gamma) & 0 \\ 0 & 0 & 1 \end{array} \right]$¶
A Choice of Gimbals¶
Click here to try this interactively
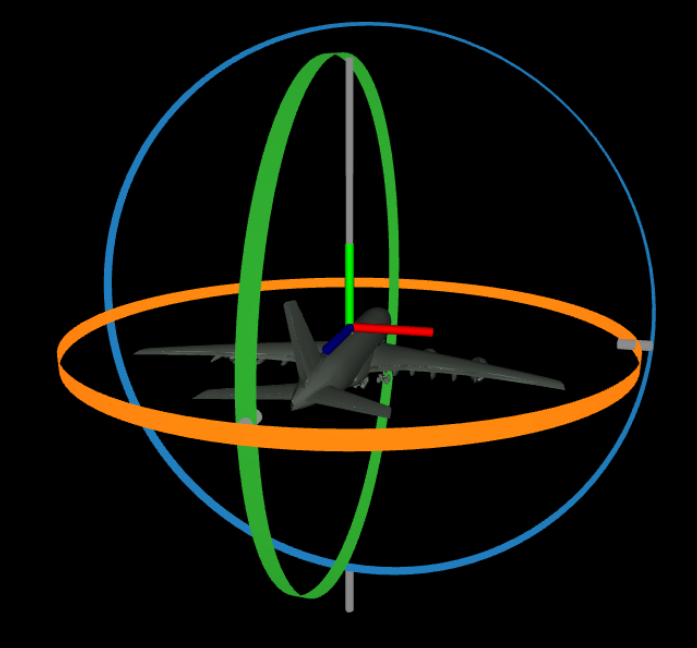
The scene graph describing our choice is shown below:
Below is the full matrix that takes local coordinates on the inner ring to world coordinates:
$R_Y(\alpha) R_X(\beta) R_Z(\gamma) = \left[ \begin{array}{ccc} c_{\alpha} c_{\gamma} + s_{\alpha} s_{\beta} s_{\gamma} & c_{\gamma} s_{\alpha} s_{\beta} - c_{\alpha} s_{\gamma} & c_{\beta} s_{\alpha} \\ c_{\beta} s_{\gamma} & c_{\beta} c_{\gamma} & -s_{\beta} \\ c_{\alpha} s_{\beta} s_{\gamma} - c_{\gamma} s_{\alpha} & c_{\alpha} c_{\gamma} s_{\beta} + s_{\alpha} s_{\gamma} & c_{\alpha} c_{\beta} \end{array} \right] $¶
NOTE: These matrices can be multiplied together in any order, and everything I'm discussing below still applies. We've chosen one of six possible orders. Have a look at the others on Wikipedia
Linear Interpolation¶
Want to do an animation for $(\alpha_1, \beta_1, \gamma_1)$ to $(\alpha_2, \beta_2, \gamma_2)$¶
The linear interpolation between both of these, where $t \in [0, 1]$, is
$(\alpha(t), \beta(t), \gamma(t)) = ( \alpha_1 (1-t) + \alpha_2 t, \beta_1 (1-t) + \beta_2 t, \gamma_1 (1-t) + \gamma_2 t )$¶
So at the beginning at time $t=0$, we have
$(\alpha(t), \beta(t), \gamma(t)) = (\alpha_1, \beta_1, \gamma_1)$¶
and at the end at time $t=1$, we have
$(\alpha(t), \beta(t), \gamma(t)) = (\alpha_2, \beta_2, \gamma_2)$¶
$R_Y(\alpha) R_X(\beta) R_Z(\gamma) = \left[ \begin{array}{ccc} c_{\alpha} c_{\gamma} + s_{\alpha} s_{\gamma} & s_{\alpha} c_{\gamma} - c_{\alpha} s_{\gamma} & 0 \\ 0 & 0 & -1 \\ c_{\alpha} s_{\gamma} - c_{\gamma} s_{\alpha} & c_{\alpha} c_{\gamma} + s_{\alpha} s_{\gamma} & 0 \end{array} \right] $¶
Using the cosine sum and sine sum identities, we se that we get the following matrix, in which $\alpha$ and $\gamma$ fight against each other to rotate in the same plane
$R_Y(\alpha) R_X(\beta) R_Z(\gamma) = \left[ \begin{array}{ccc} \cos(\alpha - \gamma) & \sin(\alpha - \gamma) & 0 \\ 0 & 0 & -1 \\ -\sin(\alpha - \gamma) & \cos(\alpha - \gamma) & 0 \end{array} \right] $¶
NOTE: A similar thing will happen with any other order I put the rotation matrices in, if I set the inner ring to have a rotation angle of 90 degrees or 270 degrees. In all cases, the outer rings will be stuck rotating in the same plane. Another way of saying this is we "lose a degree of freedom" in the rotation; we used to be able to do 3 different things with 3 different angles, but now two of them collapse to the same plane of rotation, so we can only do 2 things with the three angles
Rotation matrix -> Angles¶
It's possible to derive the angles that would realize an arbitrary rotation matrix. To see this, we'll go back to the full rotation matrix and look for some opportunities to isolate the angles
$R = R_Y(\alpha) R_X(\beta) R_Z(\gamma) = \left[ \begin{array}{ccc} c_{\alpha} c_{\gamma} + s_{\alpha} s_{\beta} s_{\gamma} & c_{\gamma} s_{\alpha} s_{\beta} - c_{\alpha} s_{\gamma} & c_{\beta} s_{\alpha} \\ c_{\beta} s_{\gamma} & c_{\beta} c_{\gamma} & -s_{\beta} \\ c_{\alpha} s_{\beta} s_{\gamma} - c_{\gamma} s_{\alpha} & c_{\alpha} c_{\gamma} s_{\beta} + s_{\alpha} s_{\gamma} & c_{\alpha} c_{\beta} \end{array} \right] $¶
In doing so, we get these equations:
$ \beta = \sin^{-1}(-R_{23})$¶
$\alpha = \tan^{-1} (R_{1, 3}, R_{3, 3})$¶
$\gamma = \tan^{-1} (R_{2, 1}, R_{2, 2})$¶
Below is an example of a random rotation matrix where we apply these formulas to get the $\alpha, \beta, \gamma$ that would realize these rotations with our gimbal system
import numpy as np
from numpy import linalg
np.random.seed(0)
R, _, _ = linalg.svd(np.random.randn(3, 3)) # A random rotation matrix
print(R)
[[-0.45996176 0.84045837 -0.28646975] [-0.86138526 -0.50065539 -0.08578823] [-0.21552406 0.20730151 0.95424078]]
beta = 180*np.arcsin(-R[1, 2])/np.pi
alpha = 180*np.arctan2(R[0, 2], R[2, 2])/np.pi
gamma = 180*np.arctan2(R[1, 0], R[1, 1])/np.pi
print(alpha+360, beta, gamma+360)
343.28987635835756 4.9213526531482215 239.83393701964994